¿Qué es un Radián?

Desde chiquitos, nosotros medimos los ángulos en grados, como en esta imagen.

Estos ángulos están bien, pero como cualquier medida impuesta por los humanos, tiene una escala arbitraria. ¿Por qué una vuelta completa son 360° y no 420°? Así que, los matemáticos inventaron una medida mejor más útil: los radianes.

Al principio, puede parecer poco intuitivo. Imaginate que tenés un círculo cualquiera con su radio $r$. Ahora, imaginate que tenemos un ángulo $\theta$. Ahora, fijate el arco $R$ formado.

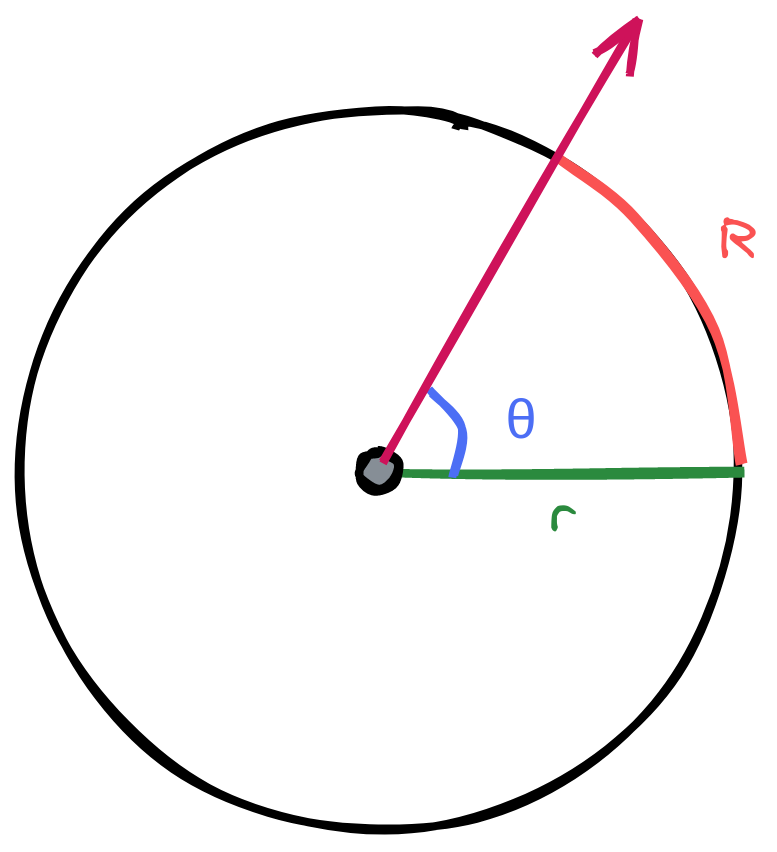
Digamos que $\theta$ es justo, justo el ángulo necesario para que la longitud de $R$ sea igual a $r$. Eso, mi gente, es un radián: el ángulo formado cuando la longitud del arco es igual al radio. Ese ángulo resulta ser $\approx 57.3°$.

Como estas proporciones se cumplen en cada círculo, usar radianes nos permite ahorrarnos varios pasos en varias cuentas (útil para MCU), ya que tenemos una relación muuuy simple entre el arco formado, el radio, y el ángulo. Si tengo 1,5 radianes, solo tengo que multiplicar radio por 1,5 y ya tengo el arco.

Ahora algo un poco más complejo. ¿Cuál sería el equivalente en radianes a 360°? Bueno… este… nosotros sabemos que el perímetro de un círculo es 3,14 veces su díametro… y el radio es la mitad del diámetro… por ende $2\pi \ast r$ es igual al perímetro… y como un radián representa un arco de la misma longitud del radio, debería ser $2\pi \text{rad}=360°$… ¡y así es!

Finalmente $\pi \text{rad}=180°$, $0.5\pi \text{rad}=90°$ y $0\text{rad}=0°$